Represent Nonlinear Dynamics Using MATLAB File for Grey-Box Estimation
This example shows how to construct, estimate and analyze nonlinear grey-box models.
Nonlinear grey-box (idnlgrey) models are suitable for estimating parameters of systems that are described by nonlinear state-space structures in continuous or discrete time. You can use both idgrey (linear grey-box model) and idnlgrey objects to model linear systems. However, you can only use idnlgrey to represent nonlinear dynamics. To learn about linear grey-box modeling using idgrey, see Building Structured and User-Defined Models Using System Identification Toolbox.
About the Model
In this example, you model the dynamics of a linear DC motor using the idnlgrey object.
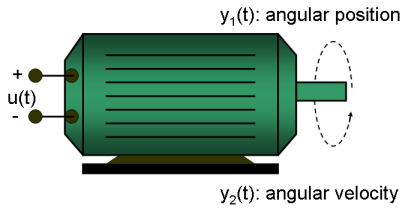
Figure 1: Schematic diagram of a DC-motor.
If you ignore the disturbances and choose y(1) as the angular position [rad] and y(2) as the angular velocity [rad/s] of the motor, you can set up a linear state-space structure of the following form (see Ljung, L. System Identification: Theory for the User, Upper Saddle River, NJ, Prentice-Hall PTR, 1999, 2nd ed., p. 95-97 for the derivation):
d | 0 1 | | 0 | -- x(t) = | | x(t) + | | u(t) dt | 0 -1/tau | | k/tau |
| 1 0 |
y(t) = | | x(t)
| 0 1 |
tau is the time-constant of the motor in [s] and k is the static gain from the input to the angular velocity in [rad/(V*s)]. See Ljung (1999) for how tau and k relate to the physical parameters of the motor.
About the Input-Output Data
1. Load the DC motor data.
load('dcmotordata');
2. Represent the estimation data as an iddata object.
z = iddata(y, u, 0.1, 'Name', 'DC-motor');
3. Specify input and output signal names, start time and time units.
z.InputName = 'Voltage'; z.InputUnit = 'V'; z.OutputName = {'Angular position', 'Angular velocity'}; z.OutputUnit = {'rad', 'rad/s'}; z.Tstart = 0; z.TimeUnit = 's';
4. Plot the data.
The data is shown in two plot windows.
figure('Name', [z.Name ': Voltage input -> Angular position output']); plot(z(:, 1, 1)); % Plot first input-output pair (Voltage -> Angular position). figure('Name', [z.Name ': Voltage input -> Angular velocity output']); plot(z(:, 2, 1)); % Plot second input-output pair (Voltage -> Angular velocity).
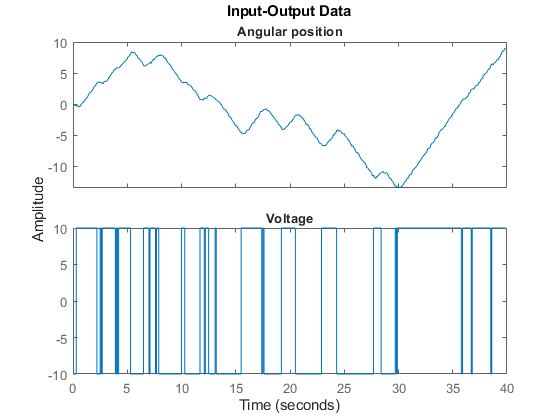
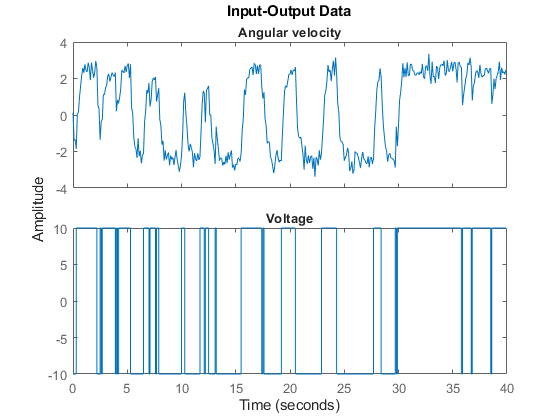
Figure 2: Input-output data from a DC-motor.
Linear Modeling of the DC-Motor
1. Represent the DC motor structure in a function.
In this example, you use a MATLAB® file, but you can also use C MEX-files (to gain computational speed), P-files or function handles. For more information, see Creating IDNLGREY Model Files.
The DC-motor function is called dcmotor_m.m and is shown below.
function [dx, y] = dcmotor_m(t, x, u, tau, k, varargin)
% Output equations.
y = [x(1); ... % Angular position.
x(2) ... % Angular velocity.
]; % State equations.
dx = [x(2); ... % Angular velocity.
-(1/tau)*x(2)+(k/tau)*u(1) ... % Angular acceleration.
];The file must always be structured to return the following:
Output arguments:
dxis the vector of state derivatives in continuous-time case, and state update values in the discrete-time case.
yis the output equation
Input arguments:
The first three input arguments must be:
t(time),x(state vector, [] for static systems),u(input vector, [] for time-series).
Ordered list of parameters follow. The parameters can be scalars, column vectors, or 2-dimensional matrices.
vararginfor the auxiliary input arguments
2. Represent the DC motor dynamics using an idnlgrey object.
The model describes how the inputs generate the outputs using the state equation(s).
FileName = 'dcmotor_m'; % File describing the model structure. Order = [2 1 2]; % Model orders [ny nu nx]. Parameters = [1; 0.28]; % Initial parameters. Np = 2. InitialStates = [0; 0]; % Initial initial states. Ts = 0; % Time-continuous system. nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ... 'Name', 'DC-motor');
In practice, there are disturbances that affect the outputs. An idnlgrey model does not explicitly model the disturbances, but assumes that these are just added to the output(s). Thus, idnlgrey models are equivalent to Output-Error (OE) models. Without a noise model, past outputs do not influence prediction of future outputs, which means that predicted output for any prediction horizon k coincide with simulated outputs.
3. Specify input and output names, and units.
set(nlgr, 'InputName', 'Voltage', 'InputUnit', 'V', ... 'OutputName', {'Angular position', 'Angular velocity'}, ... 'OutputUnit', {'rad', 'rad/s'}, ... 'TimeUnit', 's');
4. Specify names and units of the initial states and parameters.
nlgr = setinit(nlgr, 'Name', {'Angular position' 'Angular velocity'}); nlgr = setinit(nlgr, 'Unit', {'rad' 'rad/s'}); nlgr = setpar(nlgr, 'Name', {'Time-constant' 'Static gain'}); nlgr = setpar(nlgr, 'Unit', {'s' 'rad/(V*s)'});
You can also use setinit and setpar to assign values, minima, maxima, and estimation status for all initial states or parameters simultaneously.
5. View the initial model.
a. Get basic information about the model.
The DC-motor has 2 (initial) states and 2 model parameters.
size(nlgr)
Nonlinear grey-box model with 2 outputs, 1 inputs, 2 states and 2 parameters (2 free).
b. View the initial states and parameters.
Both the initial states and parameters are structure arrays. The fields specify the properties of an individual initial state or parameter. Type help idnlgrey.InitialStates and help idnlgrey.Parameters for more information.
nlgr.InitialStates(1) nlgr.Parameters(2)
ans =
struct with fields:
Name: 'Angular position'
Unit: 'rad'
Value: 0
Minimum: -Inf
Maximum: Inf
Fixed: 1
ans =
struct with fields:
Name: 'Static gain'
Unit: 'rad/(V*s)'
Value: 0.2800
Minimum: -Inf
Maximum: Inf
Fixed: 0
c. Retrieve information for all initial states or model parameters in one call.
For example, obtain information on initial states that are fixed (not estimated) and the minima of all model parameters.
getinit(nlgr, 'Fixed') getpar(nlgr, 'Min')
ans =
2x1 cell array
{[1]}
{[1]}
ans =
2x1 cell array
{[-Inf]}
{[-Inf]}
d. Obtain basic information about the object:
nlgr
nlgr =
Continuous-time nonlinear grey-box model defined by 'dcmotor_m' (MATLAB file):
dx/dt = F(t, u(t), x(t), p1, p2)
y(t) = H(t, u(t), x(t), p1, p2) + e(t)
with 1 input(s), 2 state(s), 2 output(s), and 2 free parameter(s) (out of 2).
Name: DC-motor
Status:
Created by direct construction or transformation. Not estimated.
Use get to obtain more information about the model properties. The idnlgrey object shares many properties of parametric linear model objects.
get(nlgr)
FileName: 'dcmotor_m'
Order: [1x1 struct]
Parameters: [2x1 struct]
InitialStates: [2x1 struct]
FileArgument: {}
SimulationOptions: [1x1 struct]
TimeVariable: 't'
NoiseVariance: [2x2 double]
InputName: {'Voltage'}
InputUnit: {'V'}
InputGroup: [1x1 struct]
OutputName: {2x1 cell}
OutputUnit: {2x1 cell}
OutputGroup: [1x1 struct]
Notes: [0x1 string]
UserData: []
Name: 'DC-motor'
Ts: 0
TimeUnit: 'seconds'
Report: [1x1 idresults.nlgreyest]
Performance Evaluation of the Initial DC-Motor Model
Before estimating the parameters tau and k, simulate the output of the system with the parameter guesses using the default differential equation solver (a Runge-Kutta 45 solver with adaptive step length adjustment). The simulation options are specified using the "SimulationOptions" model property.
1. Set the absolute and relative error tolerances to small values (1e-6 and 1e-5, respectively).
nlgr.SimulationOptions.AbsTol = 1e-6; nlgr.SimulationOptions.RelTol = 1e-5;
2. Compare the simulated output with the measured data.
compare displays both measured and simulated outputs of one or more models, whereas predict, called with the same input arguments, displays the simulated outputs.
The simulated and measured outputs are shown in a plot window.
compare(z, nlgr);
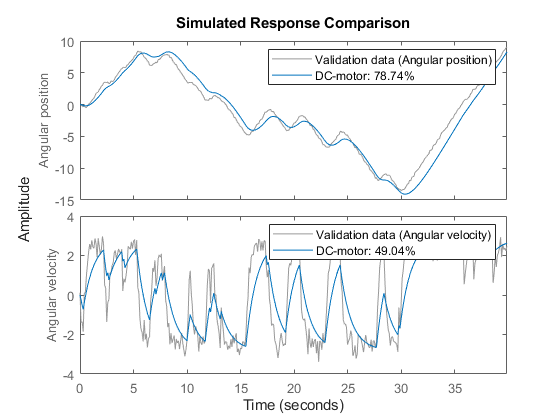
Figure 3: Comparison between measured outputs and the simulated outputs of the initial DC-motor model.
Parameter Estimation
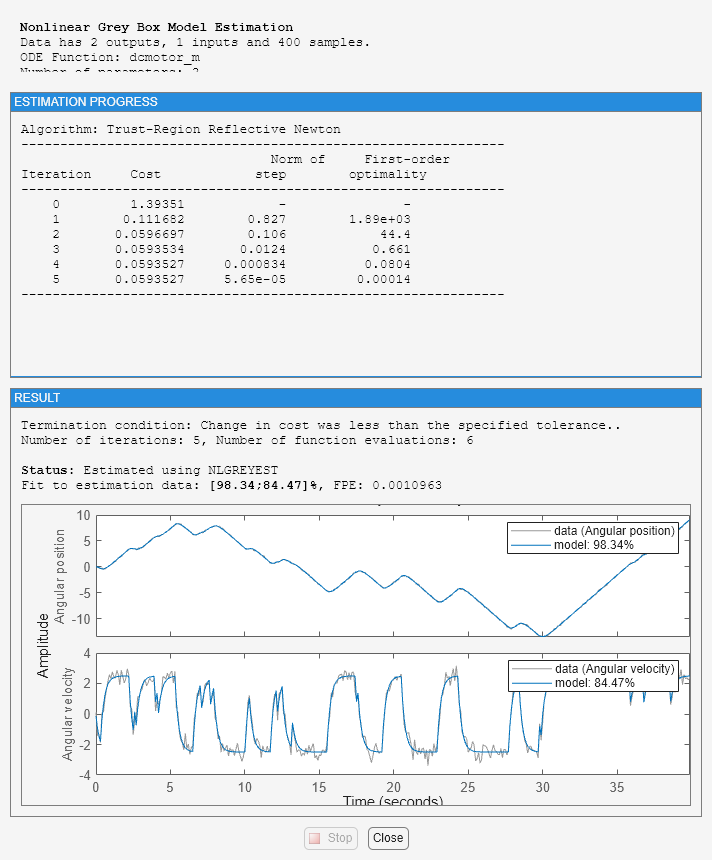
Estimate the parameters and initial states using nlgreyest, which is a prediction error minimization method for nonlinear grey box models. The estimation options, such as the choice of estimation progress display, are specified using the "nlgreyestOptions" option set.
nlgr = setinit(nlgr, 'Fixed', {false false}); % Estimate the initial states. opt = nlgreyestOptions('Display', 'on'); nlgr = nlgreyest(z, nlgr, opt);
Performance Evaluation of the Estimated DC-Motor Model
1. Review the information about the estimation process.
This information is stored in the Report property of the idnlgrey object. The property also contains information about how the model was estimated, such as solver and search method, data set, and why the estimation was terminated.
nlgr.Report
fprintf('\n\nThe search termination condition:\n')
nlgr.Report.Termination
ans =
Status: 'Estimated using NLGREYEST'
Method: 'Solver: ode45; Search: lsqnonlin'
Fit: [1x1 struct]
Parameters: [1x1 struct]
OptionsUsed: [1x1 idoptions.nlgreyest]
RandState: []
DataUsed: [1x1 struct]
Termination: [1x1 struct]
The search termination condition:
ans =
struct with fields:
WhyStop: 'Change in cost was less than the specified tolerance.'
Iterations: 5
FirstOrderOptimality: 1.4014e-04
FcnCount: 6
Algorithm: 'trust-region-reflective'
2. Evaluate the model quality by comparing simulated and measured outputs.
The fits are 98% and 84%, which indicate that the estimated model captures the dynamics of the DC motor well.
compare(z, nlgr);
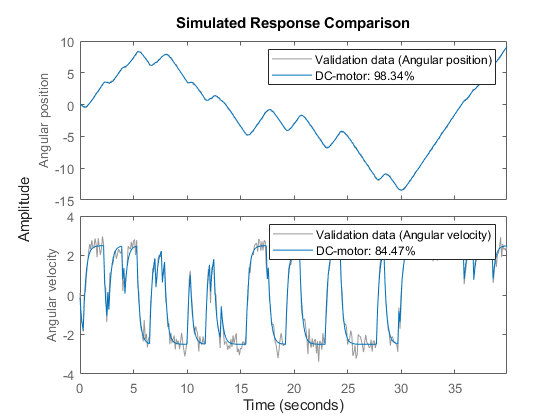
Figure 4: Comparison between measured outputs and the simulated outputs of the estimated IDNLGREY DC-motor model.
3. Compare the performance of the idnlgrey model with a second-order ARX model.
na = [2 2; 2 2]; nb = [2; 2]; nk = [1; 1]; dcarx = arx(z, [na nb nk]); compare(z, nlgr, dcarx);
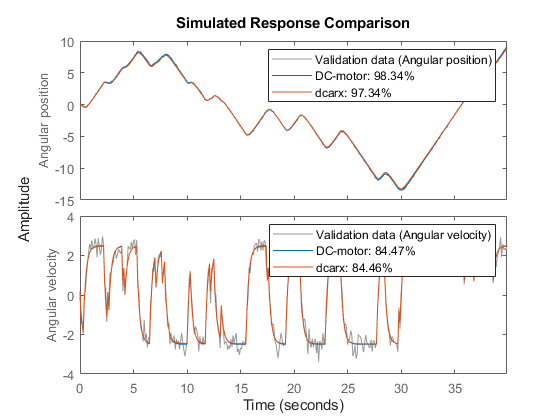
Figure 5: Comparison between measured outputs and the simulated outputs of the estimated IDNLGREY and ARX DC-motor models.
4. Check the prediction errors.
The prediction errors obtained are small and are centered around zero (non-biased).
pe(z, nlgr);
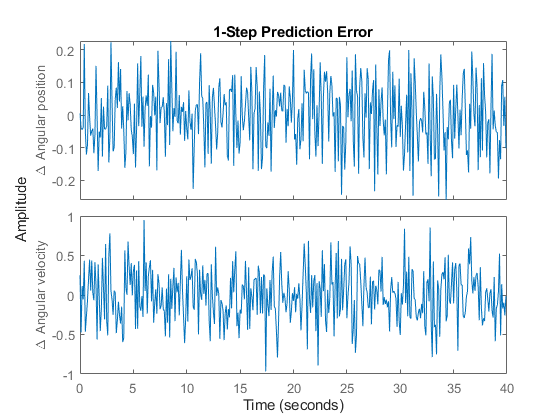
Figure 6: Prediction errors obtained with the estimated IDNLGREY DC-motor model.
5. Check the residuals ("leftovers").
Residuals indicate what is left unexplained by the model and are small for good model quality. Use the resid command to view the correlations among the residuals. The first column of plots shows the autocorrelations of the residuals for the two outputs. The second column shows the cross-correlation of these residuals with the input "Voltage". The correlations are within acceptable bounds (blue region).
figure('Name',[nlgr.Name ': residuals of estimated model']); resid(z,nlgr);
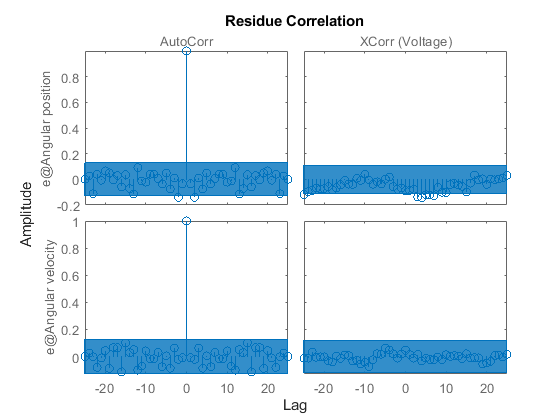
Figure 7: Residuals obtained with the estimated IDNLGREY DC-motor model.
6. Plot the step response.
A unit input step results in an angular position showing a ramp-type behavior and to an angular velocity that stabilizes at a constant level.
figure('Name', [nlgr.Name ': step response of estimated model']); step(nlgr);
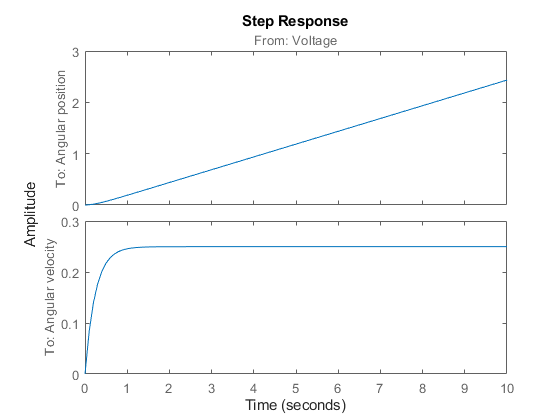
Figure 8: Step response with the estimated IDNLGREY DC-motor model.
7. Examine the model covariance.
You can assess the quality of the estimated model to some extent by looking at the estimated covariance matrix and the estimated noise variance. A "small" value of the (i, i) diagonal element of the covariance matrix indicates that the i:th model parameter is important for explaining the system dynamics when using the chosen model structure. Small noise variance (covariance for multi-output systems) elements are also a good indication that the model captures the estimation data in a good way.
getcov(nlgr) nlgr.NoiseVariance
ans =
1.0e-04 *
0.1573 0.0021
0.0021 0.0008
ans =
0.0010 -0.0000
-0.0000 0.0110
For more information about the estimated model, use present to display the initial states and estimated parameter values, and estimated uncertainty (standard deviation) for the parameters.
present(nlgr);
nlgr =
Continuous-time nonlinear grey-box model defined by 'dcmotor_m' (MATLAB file):
dx/dt = F(t, u(t), x(t), p1, p2)
y(t) = H(t, u(t), x(t), p1, p2) + e(t)
with 1 input(s), 2 state(s), 2 output(s), and 2 free parameter(s) (out of 2).
Inputs:
u(1) Voltage(t) [V]
States: Initial value
x(1) Angular position(t) [rad] xinit@exp1 0.0302675 (estimated) in [-Inf, Inf]
x(2) Angular velocity(t) [rad/s] xinit@exp1 -0.133777 (estimated) in [-Inf, Inf]
Outputs:
y(1) Angular position(t) [rad]
y(2) Angular velocity(t) [rad/s]
Parameters: Value Standard Deviation
p1 Time-constant [s] 0.243649 0.00396671 (estimated) in [-Inf, Inf]
p2 Static gain [rad/(V*s)] 0.249644 0.000284486 (estimated) in [-Inf, Inf]
Name: DC-motor
Status:
Termination condition: Change in cost was less than the specified tolerance..
Number of iterations: 5, Number of function evaluations: 6
Estimated using Solver: ode45; Search: lsqnonlin on time domain data "DC-motor".
Fit to estimation data: [98.34;84.47]%
FPE: 0.001096, MSE: 0.1187
More information in model's "Report" property.
Conclusions
This example illustrates the basic tools for performing nonlinear grey-box modeling. See the other nonlinear grey-box examples to learn about:
Using nonlinear grey-box models in more advanced modeling situations, such as building nonlinear continuous- and discrete-time, time-series and static models.
Writing and using C MEX model-files.
Handling nonscalar parameters.
Impact of certain algorithm choices.
For more information on identification of dynamic systems with System Identification Toolbox, visit the System Identification Toolbox product information page.
