ambgfun
Ambiguity and crossambiguity function
Syntax
Description
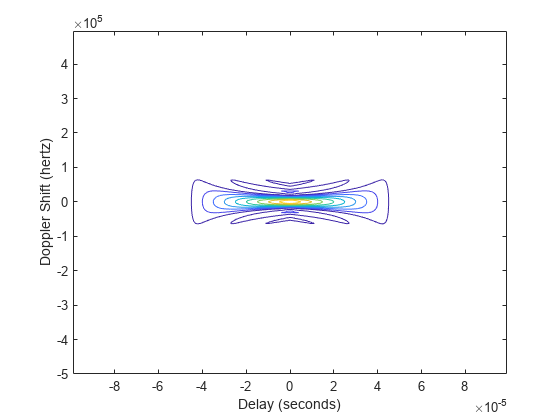
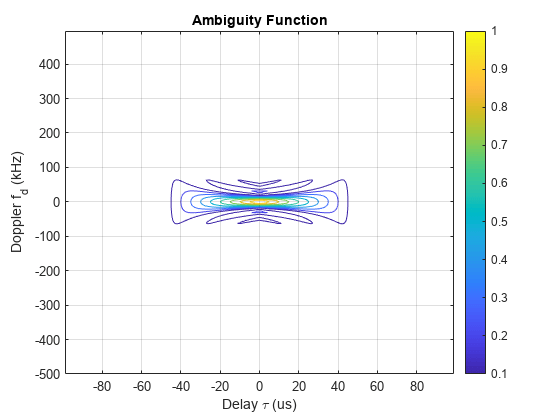
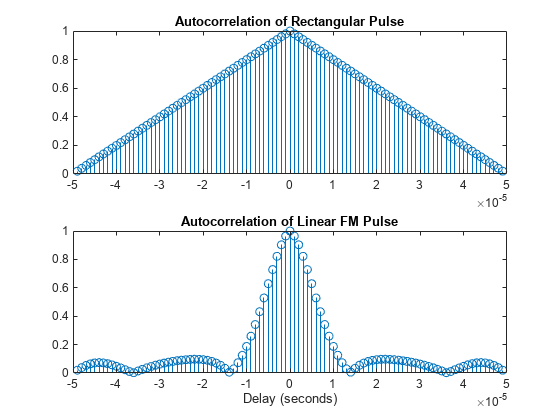
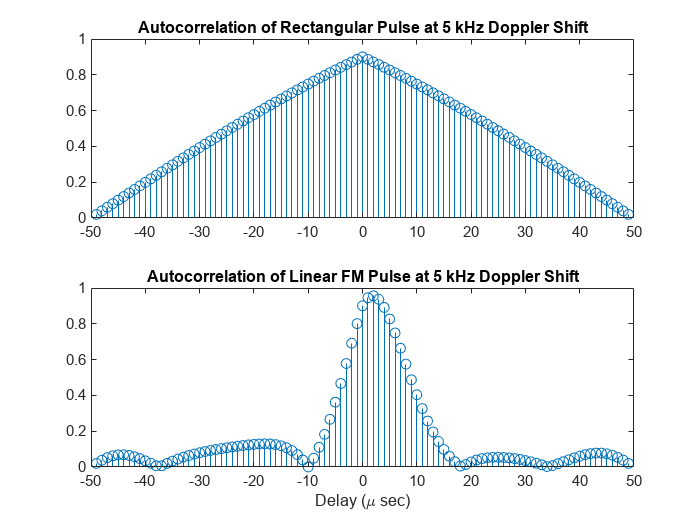
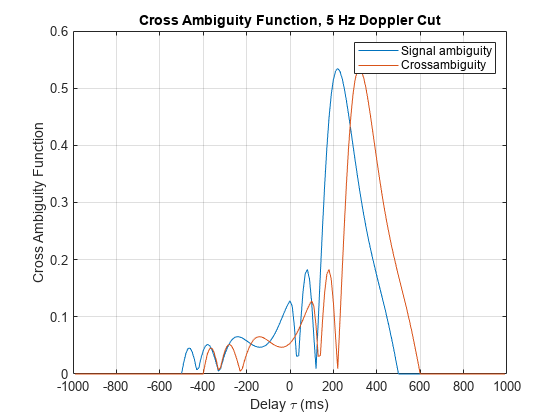
ambgfun(___), with no output arguments, plots the
ambiguity or crossambiguity function. When "Cut" is
"2D", the function produces a contour plot of the periodic
ambiguity function. When "Cut" is "Delay" or
"Doppler", the function produces a line plot of the periodic
ambiguity function cut.
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2011a