kruskalwallis
Kruskal-Wallis test
Syntax
Description
p = kruskalwallis(x)x comes from the same distribution, using the
Kruskal-Wallis test. The
alternative hypothesis is that not all samples come from the same distribution. The
Kruskal-Wallis test provides a nonparametric alternative to a one-way ANOVA. For
more information, see Kruskal-Wallis Test.
p = kruskalwallis(x,group,displayopt)
Examples
Test Data Samples for the Same Distribution
Create two different normal probability distribution objects. The first distribution has mu = 0 and sigma = 1, and the second distribution has mu = 2 and sigma = 1.
pd1 = makedist('Normal'); pd2 = makedist('Normal','mu',2,'sigma',1);
Create a matrix of sample data by generating random numbers from these two distributions.
rng('default'); % for reproducibility x = [random(pd1,20,2),random(pd2,20,1)];
The first two columns of x contain data generated from the first distribution, while the third column contains data generated from the second distribution.
Test the null hypothesis that the sample data from each column in x comes from the same distribution.
p = kruskalwallis(x)

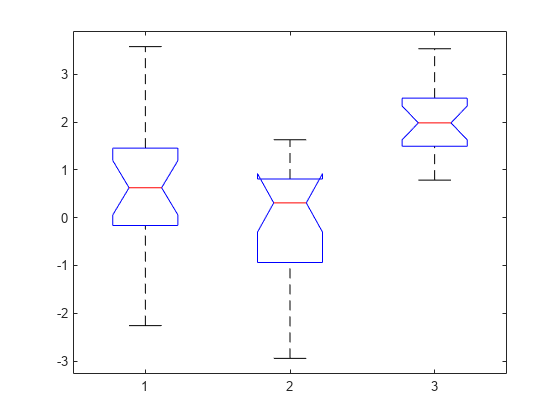
p = 3.6896e-06
The returned value of p indicates that kruskalwallis rejects the null hypothesis that all three data samples come from the same distribution at a 1% significance level. The ANOVA table provides additional test results, and the box plot visually presents the summary statistics for each column in x.
Conduct Followup Tests for Unequal Medians
Create two different normal probability distribution objects. The first distribution has mu = 0 and sigma = 1. The second distribution has mu = 2 and sigma = 1.
pd1 = makedist('Normal'); pd2 = makedist('Normal','mu',2,'sigma',1);
Create a matrix of sample data by generating random numbers from these two distributions.
rng('default'); % for reproducibility x = [random(pd1,20,2),random(pd2,20,1)];
The first two columns of x contain data generated from the first distribution, while the third column contains data generated from the second distribution.
Test the null hypothesis that the sample data from each column in x comes from the same distribution. Suppress the output displays, and generate the structure stats to use in further testing.
[p,tbl,stats] = kruskalwallis(x,[],'off')p = 3.6896e-06
tbl=4×6 cell array
{'Source' } {'SS' } {'df'} {'MS' } {'Chi-sq' } {'Prob>Chi-sq'}
{'Columns'} {[7.6311e+03]} {[ 2]} {[3.8155e+03]} {[ 25.0200]} {[ 3.6896e-06]}
{'Error' } {[1.0364e+04]} {[57]} {[ 181.8228]} {0x0 double} {0x0 double }
{'Total' } {[ 17995]} {[59]} {0x0 double } {0x0 double} {0x0 double }
stats = struct with fields:
gnames: [3x1 char]
n: [20 20 20]
source: 'kruskalwallis'
meanranks: [26.7500 18.9500 45.8000]
sumt: 0
The returned value of p indicates that the test rejects the null hypothesis at the 1% significance level. You can use the structure stats to perform additional followup testing. The cell array tbl contains the same data as the graphical ANOVA table, including column and row labels.
Conduct a followup test to identify which data sample comes from a different distribution.
c = multcompare(stats);
Note: Intervals can be used for testing but are not simultaneous confidence intervals.
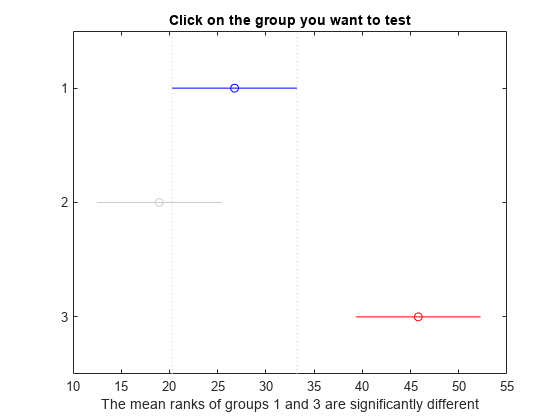
Display the multiple comparison results in a table.
tbl = array2table(c,"VariableNames", ... ["Group A","Group B","Lower Limit","A-B","Upper Limit","P-value"])
tbl=3×6 table
Group A Group B Lower Limit A-B Upper Limit P-value
_______ _______ ___________ ______ ___________ __________
1 2 -5.1435 7.8 20.744 0.33446
1 3 -31.994 -19.05 -6.1065 0.0016282
2 3 -39.794 -26.85 -13.906 3.4768e-06
The results indicate that there is a significant difference between groups 1 and 3, so the test rejects the null hypothesis that the data in these two groups comes from the same distribution. The same is true for groups 2 and 3. However, there is not a significant difference between groups 1 and 2, so the test does not reject the null hypothesis that these two groups come from the same distribution. Therefore, these results suggest that the data in groups 1 and 2 come from the same distribution, and the data in group 3 comes from a different distribution.
Test for the Same Distribution Across Groups
Create a vector, strength, containing measurements of the strength of metal beams. Create a second vector, alloy, indicating the type of metal alloy from which the corresponding beam is made.
strength = [82 86 79 83 84 85 86 87 74 82 ... 78 75 76 77 79 79 77 78 82 79]; alloy = {'st','st','st','st','st','st','st','st',... 'al1','al1','al1','al1','al1','al1',... 'al2','al2','al2','al2','al2','al2'};
Test the null hypothesis that the beam strength measurements have the same distribution across all three alloys.
p = kruskalwallis(strength,alloy,'off')p = 0.0018
The returned value of p indicates that the test rejects the null hypothesis at the 1% significance level.
Input Arguments
x — Sample data
vector | matrix
Sample data for the hypothesis test, specified as a vector or
an m-by-n matrix. If x is
an m-by-n matrix, each of the n columns
represents an independent sample containing m mutually
independent observations.
Data Types: single | double
group — Grouping variable
numeric vector | logical vector | character array | string array | cell array of character vectors
Grouping variable, specified as a numeric or logical vector, a character or string array, or a cell array of character vectors.
If
xis a vector, then each element ingroupidentifies the group to which the corresponding element inxbelongs, andgroupmust be a vector of the same length asx. If a row ofgroupcontains an empty value, that row and the corresponding observation inxare disregarded.NaNvalues in eitherxorgroupare similarly ignored.If
xis a matrix, then each column inxrepresents a different group, and you can usegroupto specify labels for these columns. The number of elements ingroupand the number of columns inxmust be equal.
The labels contained in group also annotate
the box plot.
Example: {'red','blue','green','blue','red','blue','green','green','red'}
Data Types: single | double | logical | char | string | cell
displayopt — Display option
'on' (default) | 'off'
Display option, specified as 'on' or 'off'.
If displayopt is 'on', kruskalwallis displays
the following figures:
An ANOVA table containing the sums of squares, degrees of freedom, and other quantities calculated based on the ranks of the data in
x.A box plot of the data in each column of the data matrix
x. The box plots are based on the actual data values, rather than on the ranks.
If displayopt is 'off', kruskalwallis does
not display these figures.
If you specify a value for displayopt, you
must also specify a value for group. If you do
not have a grouping variable, specify group as [].
Example: 'off'
Output Arguments
p — p-value
scalar value in the range [0,1]
p-value of the test, returned as a scalar
value in the range [0,1]. p is the probability
of observing a test statistic as extreme as, or more extreme than,
the observed value under the null hypothesis. Small values of p cast
doubt on the validity of the null hypothesis.
tbl — ANOVA table
cell array
ANOVA table of test results, returned as a cell array. tbl includes
the sums of squares, degrees of freedom, and other quantities calculated
based on the ranks of the data in x, as well
as column and row labels.
stats — Test data
structure
Test data, returned as a structure. You can perform followup
multiple comparison tests on pairs of sample medians by using multcompare, with stats as
the input value.
More About
Kruskal-Wallis Test
The Kruskal-Wallis test is a nonparametric version of classical one-way
ANOVA, and an extension of the Wilcoxon rank sum test to more than two groups. The
Kruskal-Wallis test is valid for data that has two or more groups. It compares the
medians of the groups of data in x to determine if the samples
come from the same population (or, equivalently, from different populations with the
same distribution).
The Kruskal-Wallis test uses ranks of the data, rather than numeric values, to compute the test statistics. It finds ranks by ordering the data from smallest to largest across all groups, and taking the numeric index of this ordering. The rank for a tied observation is equal to the average rank of all observations tied with it. The F-statistic used in classical one-way ANOVA is replaced by a chi-square statistic, and the p-value measures the significance of the chi-square statistic.
The Kruskal-Wallis test assumes that all samples come from populations having the same continuous distribution, apart from possibly different locations due to group effects, and that all observations are mutually independent. By contrast, classical one-way ANOVA replaces the first assumption with the stronger assumption that the populations have normal distributions.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)